Use the CUMLPMT Function in Excel to Calculate Cumulative Loan Payments

The CUMLPMT function in Excel is a financial formula used to calculate the cumulative payment for a loan over a specified period, given the interest rate, loan term, loan amount, and payment frequency. It is useful for creating an amortization schedule and determining the total payments made over the life of a loan.

Syntax

=CUMLPMT(rate, nper, pv, start_period, end_period, type)

Where:

rate: The interest rate per period.
nper: The total number of payment periods.
pv: The present value, or loan amount.
start_period: The starting payment period.
end_period:The ending payment period.
type Optional: The timing of the payment: 0 for payments due at the end of the period (default), or 1 for payments due at the beginning of the period.

The result of the CUMLPMT function is the cumulative payment made for the loan over the specified period, including both principal and interest payments.

For example

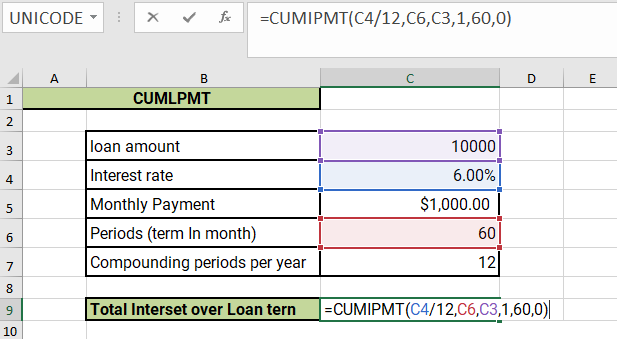
=CUMIPMT(C4/12,C6,C3,1,60,0)

The formula =CUMIPMT(C4/12,C6,C3,1,60,0)in Excel is using the CUMIPMT function to calculate the cumulative interest paid on a loan over a specified period, given the interest rate, loan term, loan amount, and payment frequency. Here's what each argument of the function represents:

C4/12:This is the first argument of the CUMIPMT function, which represents the interest rate per period. In this case, it is the annual interest rate (cell C4) divided by the number of payment periods per year (12), to get the monthly interest rate.
C6: This is the second argument of the CUMIPMT function, which represents the total number of payment periods. It is a cell reference to a cell containing the total number of payments over the life of the loan.
C3:This is the third argument of the CUMIPMT function, which represents the present value, or loan amount. It is a cell reference to a cell containing the loan amount.
1:This is the fourth argument of the CUMIPMT function, which represents the starting payment period. In this case, it is the first payment period.
60: This is the fifth argument of the CUMIPMT function, which represents the ending payment period. In this case, it is the 60th payment period.
0: This is the sixth argument of the CUMIPMT function, which represents the timing of the payment. It is set to 0, which means payments are due at the end of each period.li>

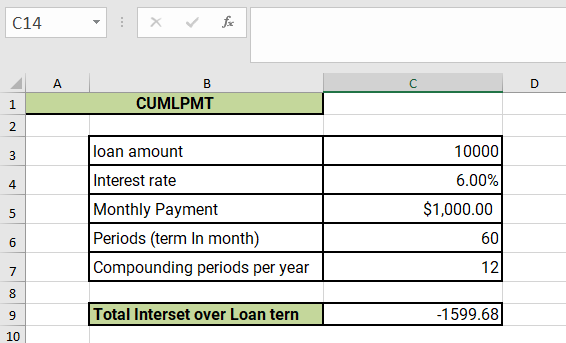
The result of this formula will be the cumulative interest paid on the loan from the first to the 60th payment period, expressed as a negative value. This means that the result of the CUMIPMT function is subtracted from the loan amount to get the total cost of the loan.

For example, if cell C4 contains an annual interest rate of 6%, cell C6 contains the total number of payments over the life of the loan of 60, and cell C3 contains the loan amount of $10,000, then the formula =CUMIPMT(C4/12,C6,C3,1,60,0)will return the total interest paid on the loan over the first 60 payment periods as a negative value.

The CUMIPMT function is a useful tool for analyzing the payment schedule of a loan and determining the total cost of the loan over its life, taking into account the interest rate and payment frequency. It is often used in financial analysis and loan management to track interest payments and evaluate the cost of different loan options.